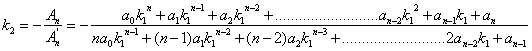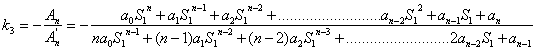----- Original Message -----
From: Ippolito Campora
Sent: Thursday, January 03, 2008 12:42 PM
Subject: equazioni polinomiali
Caro sig. Bellia, mi chiamo Ippolito Campora
e sono un chimico teorico appassionato di matematica, ho 38 anni.
Con mia grande sorpresa navigando in rete
mi sono imbattuto nel suo sito ed ho trovato il suo algoritmo per la ricerca degli
zeri reali di un polinomio.
Ebbene è identico al mio, salvo il fatto
che io riesco a risolvere equazioni polinomiali di qualsiasi grado a coefficienti
reali ma anche complessi, trovando quindi le soluzioni di una qualsivoglia equazione
polinomiale siano esse reali che complesse.
Strano ma vero sono partito dalle sue stesse
considerazioni iniziali generalizzandole poi utilizzando l'espansione in serie di
taylor ed utilizzando traslazioni primarie arbitrarie con numeri complessi; il calcolo
continuo, mi permetta, da noi adottato, mi fornisce in sequenza tutti gli zeri siano
essi reali e/o complessi di un polinomio qualunque (a coefficienti reali e/o complessi).
Le invio una copia del mio lavoro per un
parere.
Sperando di risentirla (ci spero prorpio,
perchè ci terrei molto!!), la saluto cordialmente.
dott. Ippolito Campora
Allegato:
Zeri di equazioni polinomiali in una variabile, con l’algoritmo di
t-Trasformazione ed annullamento del termine noto.
Per introdurre la: t-Trasformazione
dei polinomi, consideriamo il generico trinomio di secondo grado a coefficienti
reali: “
” e trasformiamo l’equazione algebrica relativa, dividendo per:
“
”, tutti i suoi coefficienti: → “
”.
Imponiamo di seguito, il cambiamento
di variabile: “
”, con: “
” a “un numero reale o complesso”.
Con tale sostituzione, l’equazione
di partenza diverrà:
L’ equazione: t-Trasformata, è dunque: 
Come è logico intuire se :
“
” sono gli zeri dell’equazione t-Trasformata, essi risulteranno:
“traslati”, lungo l’asse delle ascisse
e quello immaginario, delle quantità costituenti rispettivamente la parte reale
ed immaginaria di: “ 
“, che può anche essere
nulla; difatti se poniamo:
a 
Otteniamo:
a “
”
Calcoliamo gli zeri della t-Trasformata,
che scriviamo in maniera compatta: 
Ragioniamo nel modo che segue:
Troviamo quel valore di: “
”, che annulli il coefficiente: “
”, cioè in pratica risolviamo l’equazione: 
ed Inseriamo tale valore di
traslazione, nella trasformata: 
otteniamo: 
Riprendiamo adesso l’equazione
di secondo grado iniziale e cerchiamo di calcolare questa volta una sua soluzione
non più esatta, ma approssimata; per far ciò: sviluppiamo la radice del discriminante
a mezzo di una frazione continua, considerando i due casi in cui lo stesso discriminante
sia rispettivamente, maggiore o uguale a zero e minore di zero:
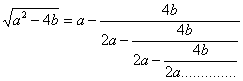
Calcolando la prima ridotta della frazione continua di cui sopra, si
ricava:
.
Inserendo poi quest’ultima, nell’espressione che ci fornisce le radici
dell’equazione di secondo grado, si ottiene:
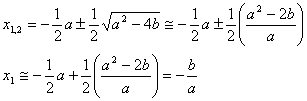
Calcolando adesso la terza ridotta dell’espressione: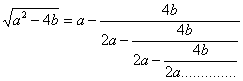, ricaviamo:
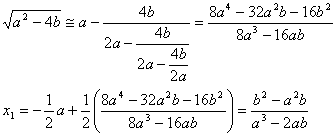
Volendo a questo punto, ripetere l’intero calcolo per il caso in cui
sia: 
‹ 0, otterremo identicamente il medesimo risultato, in quanto:
e così via per le ridotte di ordine superiore.
Se quindi, cerchiamo di calcolare in questo modo le radici complesse
approssimate dell’equazione iniziale, non otterremo alcuna stima per quest’ultime.
Il ragionamento fin qui compiuto, può darci la possibilità di escogitare
una strategia, per recuperare le radici: reali
o complesse coniugate approssimate, dell’equazione di partenza.
Quello che vogliamo fare, consiste in pratica nel generare un algoritmo
di calcolo iterativo, che simuli l’estrazione di radice quadrata del discriminante,
non più dell’equazione iniziale ma della sua prima: t-Trasformata, che riscriviamo
qui di seguito:
a 
Dobbiamo allora attribuire al parametro: “”, un valore iniziale, che potrebbe essere per il ragionamento
fatto fino a questo punto, del tutto arbitrario o meno.
Contemplando entrambi i casi, scegliamo inizialmente, un valore arbitrario
per: “”.
Ritrasformiamo adesso con un
nuovo cambiamento di variabile, la t-Trasformata precedente:
a 
Se calcolassimo esattamente
le radici della precedente, le radici dell’iniziale in: “
”, si ricaverebbero banalmente, dalla formula:
ma, ancora una volta avremmo
bisogno di attribuire al nuovo parametro: “
”, un proprio valore.
Il valore di detto parametro,
potrebbe scegliersi sempre arbitrariamente, ma la strategia non ci porterebbe da
nessuna parte.
In vece di muoverci in tal
maniera arbitraria, condizioniamo il valore di: “
”, a quello che si calcolerebbe, annullando la parte di primo
grado, dell’equazione:
ossia, risolvendo: l’equazione ridotta, seguente:
a 
Inserendo tale valore, nell’equazione:
“”, muteranno come è logico i suoi coefficienti, e l’equazione
stessa potrà riscriversi così:
Imponiamo quindi, un terzo
cambiamento di variabile, ponendo: “
”, e ripetiamo l’intera procedura.
Avremo: 
a 
a 
mentre la soluzione, dell’equazione
iniziale diverrà a questo punto: 
Iterando in questo modo e fermandoci
all’ennesima: t-Trasformata, la soluzione dell’iniziale, potrà dunque scriversi: 
Ma ancora una volta, potrebbe
sembrare un lavoro inutile, perché condizionato dalla conoscenza del valore da attribuire
alla soluzione dell’ennesima: t-Trasformata, ossia alla radice: “
”.
Se: “”, tendesse però a: zero,
al limite per: “N” che tende all’infinito, la
soluzione dell’equazione iniziale sarebbe dunque determinata, dalla sola sommatoria,
(serie in realtà, per quello che stiamo dicendo):
Fermandoci in realtà ad un
numero intero di passaggi iterativi, la soluzione approssimata sarebbe:
Quello che vogliamo dunque
scoprire e se l’algoritmo, assolva a tale compito; ciò lo faremo seguendo i primi
passi dello sviluppo iterativo, dell’equazione: “”.
[Sviluppo iterativo]:
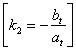
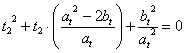a 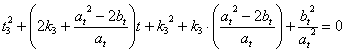a 
a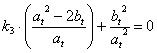
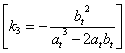a 
a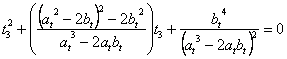 
Sommando su: “
”, si ricava:
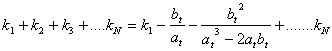
ma questi, altro non è, che
lo sviluppo della seguente formula:
(0) 
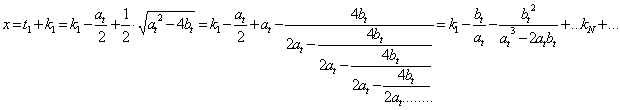
Per cui, possiamo asserire
che:
Possiamo adesso distinguere
due casi e precisamente:
(1) 
a è un numero: “reale”, arbitrario.
(2) a è un numero: “complesso”,
arbitrario.
Nel primo caso: “(1)”, se l’equazione:
“”, ha: “zeri reali”, nello sviluppo iterativo: “(0)”, tutti i
coefficienti saranno anch’essi reali e la sommatoria su: “”, ci fornirà di conseguenza, uno zero reale dell’equazione iniziale.
Se al contrario, l’equazione:
“”, ha: “zeri complessi coniugati”, lo sviluppo iterativo e la
sommatoria stessa, non andranno a convergenza su uno di essi, dato che i coefficienti
dello sviluppo nonché la sommatoria su: “”, sono entrambe reali.
Nel secondo caso: “(2)”, se
l’equazione: “”, ha: “zeri reali o complessi coniugati”, nello sviluppo iterativo:
“(0)”, tutti i coefficienti saranno: “complessi”; la sommatoria di conseguenza approssimerà
uno degli zeri: “reali o complessi coniugati”, dell’equazione iniziale.
Se dunque si cercano solo gli
zeri reali dell’equazione iniziale, ammettendo che abbia solo zeri reali, si potrà
dare a: “”, un valore arbitrario reale, o nel caso in cui, sempre nell’equazione
iniziale in: “ “, sia presente il termine di primo grado, detto valore, potrà
essere condizionato a quello che risolve l’equazione ridotta in: “”, seguente: 
a 
.
Se invece si vogliono calcolare
gli: zeri reali o complessi coniugati, dell’iniziale, si dovrà dare a: “”, un valore: complesso, del tutto arbitrario.
Analizzando ancora lo sviluppo iterativo, notiamo quanto segue:
Esiste allora un legame,
tra l’applicazione dell’algoritmo, ci fornisce in successione i valori: “ 
” e la formula generale:
a che ci restituisce i medesimi.
Questa altro non è che la
formula di: “Newton----Rhapson”.
L’applicazione della precedente,
ci indica che noi cerchiamo quei valori di: “
”, soluzioni dell’equazione in: “
”, che costituisce il termine noto della t-Trasformata, che vogliono
avere, nel valore: “nullo”, la loro prima approssimazione.
Difatti, noi non iteriamo
direttamente, sulla:
, con: 
ma bensì, la utilizziamo:
“ricorsivamente”, inserendo il valore
che ci restituisce, in tutti i termini del polinomio t-Trasformato, che poi ritrasformiamo
per poter ricavare un successivo valore del parametro, da reinserire a sua volta
nel polinomio da cui è stato generato per annullamento della parte di primo grado
del proprio termine noto, (polinomio di secondo grado in: “”) .
L’algoritmo per andare a
convergenza richiede, che nella successione:
“
”, i termini decrescano in valore assoluto, fino a raggiungere
il valore nullo al limite di infiniti cicli d’iterazione.
In tal modo essendo nullo,
l’ultimo valore di: “”, si sarà raggiunta la convergenza anche nella: “j-esima=infinito”, formula, cioè sarà:
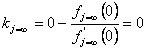
Quindi il valore: “zero”, sarà soluzione dell’equazione in:
“”, che è il termine noto
dell’ultima: “t-Trasformata”, che di
conseguenza si ridurrà di un grado.
Se ci fermiamo come è logico
ad un numero: “N”, di iterazioni, possiamo
ricavare il primo zero approssimato, dell’equazione iniziale attraverso la formula:
Il secondo zero dell’iniziale lo ricaveremo, sommando quest’ultimo,
all’opposto del coefficiente della: “
”, di primo grado, secondo lo schema:
Adesso, in maniera analoga,
per le equazioni di ed i polinomi di 3° grado, la formula della: t-Trasformata sarà
data da:
Mentre per quelle di 4° grado avremo:
In generale per una equazione di grado: “n”, si avrà:
·
Prima di procedere si sottolinea
che, la: t-Trasformazione, può evidentemente anche essere compiuta su un qualsiasi
polinomio che non abbia necessariamente, il coefficiente della variabile di grado:
“n”, pari all’unità.
·
Anche se qui si sono date le
formule valide per questo caso, la generalizzazione risulta ovvia.
·
Inoltre, per quel che riguarda il ciclo iterativo stesso, esso può
essere fermato e poi ripreso, sulla “n-esima”: t-Trasformata, per consentirci di dare a: “
”, un qualsivoglia valore arbitrario, (reale se si cercano solo
gli zeri reali o complesso per tutti gli zeri sia reali che complessi), conteggiandolo
però nella sommatoria finale che ci darà, il primo zero dell’equazione iniziale.
Traiamo ora la prima regola sulle “t-Trasformazioni”, dei polinomi:
·
I termini noti delle equazioni
trasformate, sono uguali alle equazioni da
trasformare espresse in: “”.
Passiamo ora ad un’altra
osservazione e traiamo la seconda regola sulla trasformazione dei polinomi di ennesimo
grado:
·
A partire dai termini noti
delle equazioni trasformate, gli altri coefficienti sono uguali alle derivate di
quelli a destra divise per l’esponente della “
”, di pertinenza.
Le due regole generali possono anche essere così espresse:
·
Le formule dei coefficienti di una funzione trasformata di grado: “n”, a partire dal termine noto, sono date
rispettivamente dal valore della funzione originale espressa in: “” e ordinatamente dalle derivate, prima, seconda, ...........
·
(n-1)-esima, rispetto a: “”, ciascuna divisa per il:
“fattoriale”, del grado della:
“” di pertinenza.
In conclusione dunque, la: t-Trasformazione di un polinomio, altri
non è che il suo sviluppo in: Serie di Taylor, di punto iniziale: “
”:
·
Tutto il discorso, può quindi farsi discendere dalla applicazione ricorsiva
ed iterativa dello sviluppo in serie di taylor e dall’applicazione della formula
di Newton-Rhapson ad un passo su ogni t-Trasformata.
·
Il metodo dunque, sembrerebbe ereditare, pregi e difetti dell’algoritmo
di: Newton-Rhapson, nel senso ad esempio dell’ordine di approssimazione sulle radici
dell’equazione iniziale, anche se al contempo risulta innovativo per la particolare
applicazione: ricorsiva che esso utilizza.
·
In questo senso, le traslazioni:
“”, mano a mano calcolate, ci dovrebbero restituire, un’approssimazione
sulle effettive ridotte dell’equazione di secondo grado presa inizialmente come
esempio.
·
Quindi anche al limite di infinite traslazioni, le sommatorie di queste
ultime non dovrebbero convergere sulle soluzioni esatte di qualsivoglia equazione
polinomiale in una varabile a coefficienti reali e/o complessi, ma bensì sulle soluzioni
approssimate, proprie dell’algoritmo di: Newton-Rhapson.
·
Ma a differenza di quest’ultimo, il nostro metodo utilizza la formula
di: Newton-Rhapson, ad una passo e ricorsivamente su, teoricamente parlando: infinite
t-Trasformate.
Questo nuovo modo di operare,
abbatte l’ordine di approssimazione dell’algoritmo stesso, (Newton-Rhapson), sempre
che bene inteso, si prendano i numeri reali o complessi che rappresentano le traslazioni:
“”, con quante più cifre decimali possibile, con l’utilizzo verosimilmente
di un calcolatore elettronico.
Le soluzioni o: “zeri”, delle precedenti, saranno quindi dati dalle
formule:
In generale quindi, per qualunque grado, varranno le formule:
.
I valori: “
”, in ultima analisi possono sempre pensarsi, come: traslazioni
nell’asse reale del dominio della funzione associata all’equazione iniziale, quando
questi sono reali, essi traslano passo-passo, la funzione “orizzontalmente”, verso
l’origine degli assi cartesiani; ecco perché le: sommatorie delle traslazioni, coincidono con gli zeri reali dell’equazione
iniziale.
Nel caso i “”,siano: complessi,
una tale rappresentazione grafica non può costruirsi, perché l’equazione stessa
viene trasformata in una equazione a: coefficienti
complessi.
Per quel che riguarda la ricerca contemporanea degli zeri reali e complessi
coniugati dell’equazione iniziale in: “”, attraverso traslazione complessa, bisogna però, tenere conto
di quanto segue:
(1)
nel passaggio dalla t-Trasformata di grado: “n”, a quella di grado: “n-”, potrebbe presentarsi con coefficienti reali; in tal caso si
rende necessaria, una ulteriore traslazione primaria complessa da compiersi nell’equazione
di grado: “n-
(2)
Si possono poi presentare i seguenti casi che riguardano i coefficienti
delle t-trasformate di qualunque grado: (a) il coefficiente dell’incognita di primo
grado potrebbe ad un certo punto del ciclo iterativo rendersi nullo; (b) il valore
della traslazione: “”, potrebbe ad un certo punto del ciclo iterativo, non diminuire
più in termini del suo modulo.
Quando allora, questi casi
si presentano, si può sempre ovviare: ritraslando
arbitrariamente, prima di procedere con il ciclo iterativo, con una quantità
complessa ancora una volta arbitraria.
Per rendere in un certo senso,
meno arbitraria l’eventuale scelta di queste traslazioni aggiuntive, si può convenire
di scegliere allorché questi casi si presentino, lo stesso valore complesso per
la traslazione arbitraria stessa, ad esempio prendendo per: “
”, il valore unità, cioè: 
, conteggiando come è ovvio tali valori aggiuntivi stessi, nelle
sommatorie finali, che ci restituiscono gli zeri reali e/o complessi coniugati dell’equazione
iniziale in: “”.
Questa eventualità potrebbe
sembrare limitante nei confronti del metodo stesso, ma in effetti, la probabilità
che tali casi, si presentino più volte e contemporaneamente è estremamente bassa,
come risulta anche dall’analisi degli esempi numerici che seguiranno.
In ogni caso, ciò non toglie
potenzialità al metodo, che prima o poi ci fornirà comunque tutti gli zeri approssimati,
dell’equazione iniziale.
Programmando il metodo, in
linguaggio per calcolatore elettronico, il software che si produrrebbe, farebbe
il controllo sui coefficienti e ritraslerebbe automaticamente questi ultimi, quando
necessario.
Costruiamo adesso, degli esempi
espliciti per testare il metodo illustrato.
Sia da risolvere l’equazione:
“
” a 
[Sviluppo iterativo]:
Sia da risolvere l’equazione:
“
”
[Sviluppo iterativo]:
È logico che se spingessimo
oltre l’iterazione, l’accordo con il valore esatto del primo zero dell’equazione,
migliorerebbe sensibilmente e il risultato influirebbe sulla seconda radice, facendola
risultare più precisa.
Sia da risolvere l’equazione:
“
”
[Sviluppo iterativo]:
Sia da risolvere l’equazione:
“
”
Essa ha per radici due numeri
complessi coniugati, che sono dati rispettivamente da: “
”.
La: “t-Trasformata”, è dunque:
[Sviluppo iterativo]:
Allo stesso risultato si sarebbe
pervenuti, utilizzando la traslazione primaria coniugata: “
”.
Se al contrario assumiamo come
traslazione primaria un numero reale per: “
”, l’iterazione non andrà a convergenza, sugli zeri complessi,
come si evince da quanto segue:
Il termine noto delle iterate,
aumenta sempre in valore assoluto ed il metodo giustamente fallisce, in quanto l’equazione
principale non ha zeri reali.
Sia da risolvere l’equazione: “
“
”
[Sviluppo iterativo]:
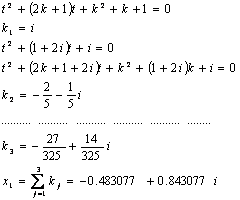
Fermandoci già alla terza iterazione,
l’accordo con le soluzioni esatte, comincia a manifestarsi palese e continuando
ad iterare, otterremo miglior convergenza.
Proviamo adesso, la convergenza
del metodo, direttamente su di un equazione a coefficienti complessi, come la seguente: “
”
[Sviluppo iterativo]: 
Applichiamo il metodo, all’equazione
che si ottiene dal prodotto dei seguenti binomi e che risulta a coefficienti complessi: “
”
[Sviluppo iterativo]:
In questo semplice caso, la
sola prima iterazione ci ha condotto direttamente alla soluzione esatta.
Risolviamo adesso tre equazioni
di grado superiore al secondo e precisamente: una cubica a coefficienti reali e
zeri reali e due cubiche a coefficienti reali aventi, due zeri complessi coniugati
ed uno zero reale:
Sia da risolvere l’equazione: “
”
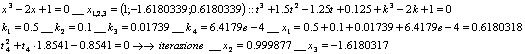
Sia da risolvere l’equazione: “
”
Sia da risolvere l’equazione: “
”
A questo punto, proviamo a
risolvere iterativamente nel campo complesso, ossia imponendo una: primaria traslazione complessa arbitraria,
un’equazione che abbia esclusivamente zeri reali, come la seguente:
Possiamo dunque asserire la validità e la completa generalità del metodo
iterativo, che indicheremo come:
[Metodo di Annullamento del Termine Noto] ⇔ [M.A.T.N.]
Quest’ultimo previa: “t-Trasformazione”, dei polinomi che costituiscono
le equazioni da risolvere, è applicabile indipendentemente dal fatto che le equazioni
stesse abbiano: coefficienti reali e/o complessi
così come i loro: zeri.
Dott. Ippolito Campora
----- Original Message -----
From: NGBellia
To: Ippolito Campora
Sent: Tuesday, December 04, 2007 3:41 PM
Subject: Re: equazioni polinomiali
Egregio dott. Campora.
Complimenti!
Ho qualche problema con l'apertura delle
formule, che risolverò in alcuni giorn, dopo di che, se ne sarò capace Le esprimerò
il mio parere.
Con stima, Nicolò Giuseppe Bellia
----- Original Message -----
From: Ippolito Campora
Sent: Saturday, December 08, 2007 5:02 PM
Subject: eq.polinomiali
Caro sig. Bellia, sono molto contento che
mi abbia risposto...io nonostante la mia età mi ritengo un teorico vecchio stampo,
uno da carta e matita per intenderci e non ho mai avuto grande passione per i computer
anche se mi rendo conto del loro valore intrinseco negli ambienti di calcolo numerico
qual'è anche il mio (mecc.quantistica), grafico ecc...visto che a quanto pare lei
li utilizza con disinvoltura, se, quando sarà riuscito ad aprire le formule scritte
con word, vorrà implementare il suo programma anche con le mie idee ne sarei grandemente
felice...la autorizzo quindi, se lo riterrà opportuno, a servirsene per completare
il suo ed il mio lavoro...
cordiali saluti ...mi auguro proprio di
risentirla..
dott. Ippolito Campora.
----- Original
Message -----
From: NGBellia
To: Ippolito Campora
Sent: Sunday, December 09, 2007 1:19 AM
Subject: Re: eq.polinomiali
Egregio
dott. Campora.
Per aiutarmi
a entrare nello spirito del Suo lavoro, La prego di ripetermi l'esempio sotto riportato,
sviluppato con il Suo metodo.
Cordialità,
Nicolò Giuseppe Bellia
----- Original Message -----
From: Ippolito Campora
Sent: Tuesday, December 25, 2007 3:17 PM
Subject: eq.polinomiali
Alla cortese attenzione di N.G.Bellia
Egregio
Sig. Bellia mi scuso per il silenzio di questi giorni ma sono stato a Siena e non
ho avuto accesso ad un computer per leggere la posta, poi ho anche avuto problemi
con il mio che si è ammalato (virus) e non ho potuto risponderle.
Innanzi tutto
auguri di buon natale e per il nuovo anno; in secondo luogo per rispondere alla
sua ultima E-mail, le scrivo quanto segue:
Il mio metodo
si serve dello sviluppo in serie di Taylor dell’equazione polinomiale data sia essa
a coeff.
Reali e/o
Complessi così come le sue radici; si introduce come punto iniziale dello sviluppo
un valore arbitrario complesso; l’equazione che io chiamo t-Trasformata (t sta per
traslazione nel campo complesso), si trasforma nella equivalente a coefficienti
complessi se in partenza ha tutti i coefficienti reali; se invece essa è gia a coeff.complessi
la traslazione primaria arbitraria è necessaria solo se il coefficiente della variabile
di primo grado è nullo, dicasi lo stesso se l’equazione ha coefficienti tutti reali
e quello della variabile di primo grado nullo.
Lei continua
a chiamare “x” la variabile indipendente del polinomio, in realtà mi scuso ma sono
sicuro che lei lo sappia, la variabile indipendente deve cambiare etichetta, io
la chiamo “t” ossia: “traslata di x”, “x=t+k”, perchè se ciò vale per le radici, vale anche per tutti gli
altri punti del dominio della funzione.
Io calcolo
poi un secondo valore per “k” dato dall’opposto del rapporto dei due nuovi coefficienti
termine noto e quello della “t” di primo
grado valutati nel punto k=zero.
In tal modo
iterando e calcolando di volta in volta tutti i coefficienti del polinomio t-Trasformato,
ossia inserendo i valori di “k” nelle espressioni delle derivate dello sviluppo
di Taylor, inseguo quel valore di “k” che renderebbe nullo l’ennesimo termine noto
della t-Trasformata datami dal ciclo continuo di iterazione.
In parole
povere è come se scrivessi: “N” “t-Trasformate” i cui coefficienti sono valutati
ossia calcolati inserendo il valore di “k” della “N-1esima”.
Se si riscontrassero
problemi di convergenza, ossia ad esempio la derivata prima in “k” si annulla, oppure
in valore assoluto “k” smette di decrescere, ritraslo di nuovo arbitrariamente in
generale sempre nel campo complesso e ricomincio fino a converge verso lo zero del
valore di “k”; sommando infine tutte le traslazioni “k”, ottengo la prima radice
sia essa reale o complessa e conseguentemente la t-Trasformata abbassata di un grado,
su cui opero analogamente per calcolare la sua prima radice.
La prima
sommatoria in “k” è la prima radice dell’equazione originale come lei mi insegna,
la seconda è quella della t-Trasformata abbassata di un grado più la prima sommatoria
in “k” ossia la prima radice calcolata per l’equazione originale.
Il mio ed
il suo metodo sono equivalenti, in tutte le loro varianti applicative; ad esempio:
Mi sono permesso
di riadattare il suo calcolo continuo per le radici reali a tutte le radici reali
e complesse di un polinomio qualsiasi.
Come di sotto
riportato lei calcola le traslazioni ”k” e poi le somma reinserendole sempre nella
stessa formula per il calcolo delle successive; in questo modo lei ma anche io possiamo
abbattere gli errori di arrotondamento nel calcolo dei coefficienti delle t-Trasformate;
operare in questo modo è dunque più esatto e coincide esattamente con l’applicazione
della formula di Newton, in quanto sommare le traslazioni e reinserirle sempre nella
stessa formula equivale a compiere il ciclo iterativo del metodo di Newton.
La nostra
innovazione sta nel fatto invece, di servirsi di un qualsiasi punto iniziale per
cominciare l’iterazione stessa e di riprenderla in modo continuo se essa presentasse
problemi di convergenza, come quelli da me sopra menzionati.
Sembrerebbe
dunque una inutile ripetizione di un metodo gia esistente, in effetti in parte lo
è; ma il nostro modo di calcolare le radici, ovvia proprio a quei problemi di convergenza
del metodo originale, che costringerebbero a ripartire da capo e per tentativi da
un nuovo punto iniziale più vicino alla prima radice dell’equazione polinomiale
originale.
Passando
poi da traslazioni o punti iniziali reali arbitrari, a quelli nel campo complesso
si ha l’opportunità di valutare tutte le radici di un qualsiasi polinomio a coefficienti
sia reali, che reali e/o complessi con lo stesso errore di arrotondamento, proprio
del metodo originale di Newton.
Cordiali
saluti e spero proprio i risentirla.
Dott. Ippolito
Campora
Algoritmo per il calcolo degli zeri di equazioni polinomiali a coefficienti
reali e/o complessi
|
1.
|
Sia data la generica equazione
polinomiale a coefficienti reali e/o complessi: |
|
2.
|
Sviluppiamo in serie di
Taylor la precedente:
|
|
3.
|
Il termine noto dell’equazione
t-Trasformata è: |
|
4.
|
Gli altri coefficienti
sono dati rispettivamente dalle derivate prima, seconda,… .(n-2)esima, (n-1)esima, ciascuna divisa per
il fattoriale della n di pertinenza:
|
|
5.
|
Se l’equazione è a coefficienti
reali o a coefficienti reali e/o complessi e se in entrambi i casi, se ha nullo
il coefficiente: “
Stessa cosa dicasi per
un equazione a coefficienti tutti reali e tutti non nulli. |
|
6.
|
Sostituiamo
questo valore a “k” e ricaviamo un secondo valore “k2”:
|
|
7.
|
Sommiamo i due primi valori
di “k”:
|
|
8.
|
Calcoliamo dunque un terzo
valore per “k”:
|
|
9.
|
Sommiamo i due precedenti
valori:
|
|
10.
|
Si continua analogamente
alla 8) e alla 9) finché il numeratore della 8) diventa nullo, cioè:
Se a un certo punto dell’iterazione,
si dovesse annullare il denominatore della 8), o se il rapporto della 8) non dovesse
tendere, in valore assoluto a zero, si introduce arbitrariamente un ennesimo valore
in generale complesso per la somma parziale “S” e si ricomincia iterando analogamente
fino a convergenza allo zero per la 8) |
|
11.
|
|
|
12.
|
Si sostituisce: “ Si passa così al calcolo
delle successive radici con lo stesso procedimento sopra esposto. |
”, trasliamo arbitrariamente nel campo complesso la precedente,
attribuendo a: “k”, un primo valore complesso tale che non si annulli la derivata
prima di: “
”, cioè:
Il
calcolo delle radici dell’esempio che lei mi ha dato, mi fornisce i valori:
1,2,3,4,5
tutti
reali
sono
partito da una traslazione arbitraria complessa: k=i
ad
esempio per la ridotta di quarto grado si ha:
|
A*x^4+B*x^3+C*x^2+D*x+E=0 |
t^4+t^3*(4*K+a)+t^2*(6*K^2+3*a*K+b)+t*(4*K^3+3*a*K^2+2*b*K+c)+K^4+a*K^3+b*K^2+c*K+d=0 |
|
A |
a(iterazione)=4*k+a |
|
1,000000000000000E+00 |
-6,00000000000017-3,34825708709764E-013i |
|
B |
b(iterazione)=6*k^2+3*a*k+b |
|
-1,400000000000000E+01 |
11,0000000000008+1,64063146838923E-012i |
|
C |
c(iterazione)=4*K^3+3*a*K^2+2*b*K+c |
|
7,100000000000000E+01 |
-6,00000000000081-2,21156633496361E-012i |
|
D |
d(iterazione)=K^4+a*K^3+b*K^2+c*K+d |
|
-1,540000000000000E+02 |
-2,79752677552878E-017+1,29073494393346E-017i |
|
E |
K(n)=-d(n)/c(n) |
|
1,200000000000000E+02 |
-4,66254462587988E-018+2,1512249065572E-018i |
|
A/A |
a(n+1)=4*k+a(n) |
|
1,000000000000000E+00 |
-6,00000000000017-3,34817103810138E-013i |
|
a=B/A |
b(n+1)=6*k^2+3*a(n)*k+b(n) |
|
-14 |
11,0000000000008+1,64059274634091E-012i |
|
b=C/A |
c(n+1)=4*K^3+3*a(n)*K^2+2*b(n)*K+c(n) |
|
71 |
-6,00000000000081-2,21151900801567E-012i |
|
c=D/A |
d(n+1)=K^4+a(n)*K^3+b(n)*K^2+c(n)*K+d(n) |
|
-154 |
0 |
|
d=E/A |
a(n+1)=4*k+a(n) |
|
120 |
-6,00000000000017-3,34825708709764E-013i |
|
K(primaria) |
b(n+1)=6*k^2+3*a(n)*k+b(n) |
|
1i |
11,0000000000008+1,64063146838923E-012i |
|
4*k+a |
c(n+1)=4*K^3+3*a(n)*K^2+2*b(n)*K+c(n) |
|
-14+4i |
-6,00000000000081-2,21156633496361E-012i |
|
6*k^2+3*a*k+b |
d(n+1)=K^4+a(n)*K^3+b(n)*K^2+c(n)*K+d(n) |
|
65-42i |
-2,79752677552878E-017+1,29073494393346E-017i |
|
4*K^3+3*a*K^2+2*b*K+c |
K(n) |
|
-112+138i |
0,78890717994175-0,277953653286058i |
|
K^4+a*K^3+b*K^2+c*K+d |
0,561732002044642-0,219189285793531i |
|
50-140i |
0,379479507527631-0,180122074988596i |
|
|
0,223544410948395-0,156724692026356i |
|
|
7,42889701250208E-002-0,130230408047683i |
|
|
-2,65869437616999E-002-3,95955007084632E-002i |
|
|
-1,34158316330296E-003+3,83454892437007E-003i |
|
|
-2,35440213945274E-005-1,89357084029503E-005i |
|
|
3,58917687668282E-010+1,63463391869982E-009i |
|
|
-4,66254462587988E-018+2,1512249065572E-018i |
|
|
1,99999999999996-8,60999358495355E-014i |
|
|
x1=1.99999999999996-8.60999358495355E-014i=2 |
|
|
|
----- Original Message -----
From: NGBellia
To: Ippolito Campora
Sent: Wednesday, December 26, 2007 7:26 PM
Subject: Re: eq.polinomiali
Egregio dott. Campora.
Ho ricevuto l'allegato: "algoritmo
2 zeri di polinomi".
Il Suo metodo è ineccepibile e vantaggioso,
nonché equivalente al mio, ed in più permette di ricavare le radici complesse.
La matematica non è la mia professione,
ma la amo e me ne servo.
Le chiedo l'autorizzazione a pubblicare
il nostro scambio di lettere nella mia pagina www.bellia.com
rendendolo prelevabile , in modo da arricchire il materiale messo gratuitamente
a disposizione degli studiosi.
Ho apprezzato la Sua lucidità e sono certo
che essa Le permetterà di raggiungere alti obiettivi scientifici.
Se un giorno avrò il piacere di icontrarLa
potremo parlare di elettrochimica dato che ho dovuto occuparmene per realizzare
il mio generatore di gas ossidrico, risolvendo tutti i problemi relativi.
Ciò in quanto la chimica dell'idrogeno
si prospetta di grande utilità sociale.
Oltre alla matematica, quale problema scientifico
attualmente La appassiona e impegna professionalmente?
La mia vita è stata un innamoramento continuo
verso varie Idee.
Cordiali saluti, Nicolò Giuseppe Bellia
From: Ippolito Campora
Sent: Thursday, December 27, 2007 2:58 PM
Subject: ippolito campora
A questo punto mi permetta di chiamrla:
Caro Sig.Bellia..
Egregio....
è così informale!!
Sono contento di averla conusciuta per
il momento solo per via telematica; la autorizzo come già detto in una precedente
E-mail a servirsi del mio lavoro in ogni modo lei riterra opportuno e di conseguenza
anche del nostro scambio di E-mail.
Come le ho scritto io sono un chimico teorico
il mio campo è la meccanica quantisitica, ormai credo di essere più un fisico che
un chimico, non solo per aver dato esami anche di quest'ultima facoltà, ma indubbiamente
per la mia attitudine mentale al lavoro di teorico puro.
Molti guardano al chimico come lo scienziato
della sperimentazione pura, colui che vive e ragiona in laboratorio..bè non è questo
il mio caso...una parte della chimica che si pone le domande: su come e perchè atomi
e molecole si danno la pena di esistere è alquanto sottovalutata nonchè snobbata,
anche in campo accademico..mi creda....
Non mi sono mai occupato di elettrochimica
ad alto livello, ma da studente avevo elaborato un metodo per la determinazione
dei coefficienti di attività e delle costanti d'equilibrio per via potenziometrica,
attraverso interpolazione non lineare sulle funzioni Volume-pH, derivate dal bilancio
di carica...forse un vano tentativo per dare senso più compiuto al concetto di attività
dei soluti...i calcoli però erano alquanto confortanti e gli sguardi dei miei docenti
conseguenza diretta: stupore, un pò di stizza come a dirmi: come mai non ci ho pensato
prima io? forse è anche per questo che non mi è stato possibile inserirmi come ricercatore
all'università.
Suppongo che i miei appunti su vare questioni
della chimica (termodinamica statistica, chimica teorica, matematica, fisica ecc..),
girino ancora fra gli studenti della mia ex facolta...
Non voglio sembrarle un presuntuoso..ma
la scienza è la mia vita, non riesco a non pensare e ripensare a un problema finchè
non ho trovato un qualche tipo di soluzione e ne ho parecchi che mi ronzano per
la mente al momento, sia in campo chimico, che fisico ma anche matematico, (sopratutto
matematico!!).
Le voglio riporatre una frase di Einstein
che probabilmente calza a pennello a tutti e due (quanto meno di certo a me!!):
Sono convinto che, per mezzo di costruzioni
puramente matematiche, sia possibile scoprire i concetti che ci danno la chiave
per comprendere i fenomeni
naturali, nonchè i principi
che legano tali concetti tra loro.
L'esperienza resta, naturalmente l'unico
criterio per controllare la validità di una costruzione puramente matematica, ma
è nella matematica che risiede in vero, il principio creativo...
Al di là dei titoli accademici che si rivelano
quasi sempre sterili etichette, sono sicuro che io e lei possediamo quella rara
qualità, simbolo principe di chi si occupa di scienza, che è la semplice: Curiosità...
il motore primo, come lo chiamo io...
Gas ossidrico?..bè sembra proprio interessante..adesso
sono curioso di saperne da lei di più, se vorrà farmene partecipe...tramite E-mail
però credo sia un pò complicato...
Se non ho capito male, lei abita a Tarquinia..non
sò al momento dove si trovi con precisione..suppongo in provincia di Roma...
Con tutta probabilità io dovrei tornare
in provincia di Siena, dove lavora la mia fidanzata tra la fine di Gennaio o la
metà di Febbraio..magari se le farà piacere potremo fare un salto da lei in uno
dei fine settimana di quei mesi...
In ogni caso, lo ribadisco è stato un vero
piacere chiaccherare con lei delle nostre comuni questioni...
Mi auguro di risentirla..le rimando gli
auguri delle fetività natalizie..
Spero a presto, cordialmente:
Ippolito Campora.
----- Original Message -----
From: NGBellia
To: Ippolito Campora
Sent: Friday, December 28, 2007 6:20 PM
Subject: Re: ippolito campora
Carissimo dott. Campora.
La ringrazio sentitamente per il contenuto della Sua lettera.
Sarò felice di incontrarLa quando potrà.
Vivo in una mia tenuta in Tarquinia (VT).
E' ormai da qualche anno che non mi impegno più in elaborazioni formali che, dati i miei 76 anni, ora mi stancano; mentre procedo con crescente piacere a livello intuitivo-immaginativo.
Dalla mia pagina Le sarà risultato il campo dei miei interessi.
Concepisco come una parte importante della vita la ricerca intuitiva di Idee in connessione con le esperienze.
Vengo compensato dal godimento della bellezza che ogni vera Idea ha vitalmente in sé.
Passo ore ed ore in lieta compagnia dell'equazione di terzo grado, manipolandola immaginativamente con i miei teoremi.
In passato mi sono occupato di scienza delle costruzioni (cemento armato , realizzando un programma in basic che in 20 minuti (primo computer olivetti) progettava una intera struttura in cemento armato con disegni per il cantiere.
Ho trovato le formule di progetto della Pressoflessioe (cemento armato) (mancanti).
Il godimento estetico è stato il compenso.
Sulla Teoria della Conoscenza concordo con la via a suo tempo seguita da Goethe e illustrata mirabilmente da Rudolf Steiner, il cui libro LA FILOSOFIA DELLA LIBERTA' (prelevabile) considero come l'opera filosofica più grande di tutti i tempi.
Quando mio figlio, che si occupa della Pagina, tornerà da una breve vacanza in Austria, inserirò le nostre lettere in www.bellia.com .
Grazie e a presto, Nicolò Giuseppe Bellia